Physics behind the project
Black Holes have always been objects of interest to everyone, from scientists to lovers of science fiction. Even though these objects were proposed some decadesa go, it was only recently that we were finnaly able to observe them in the Event Horizon Collaboration, and with these new images, the interest in them seems to have been rekindled, our interest included. So, we decided to work trying to simulate the photograph of a Black Hole, something that was already proposed many years ago (as a reference, check [1]) and that can reproduce results very similar to the ones captured by the telescopes here on Earth.
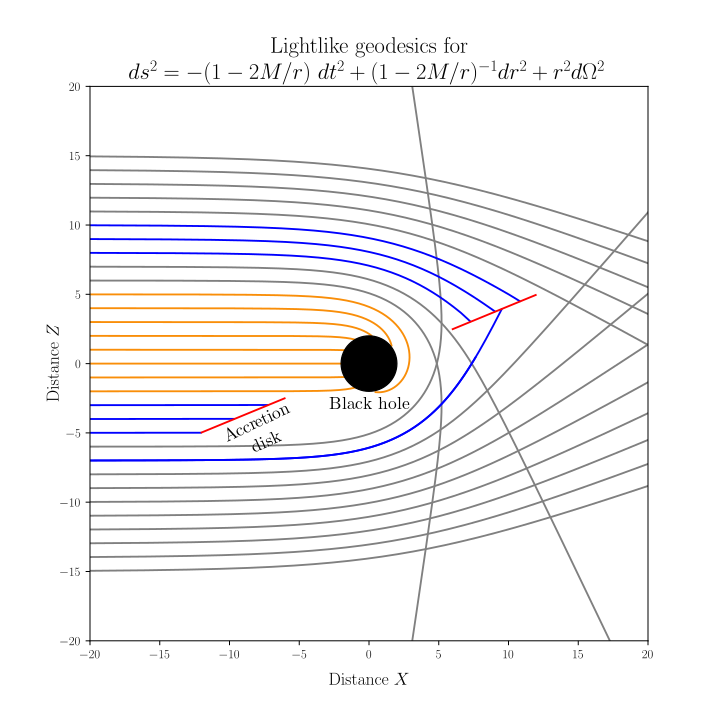
In this project, we consider only Schwarszchild Black Holes, with metric given by $$ds^2 = -\left(1-\frac{2M}{r}\right)dt^{2} + \left(1-\frac{2M}{r}\right)^{-1} + r^{2}(d\theta^{2} + sin^{2}(\theta)d\phi^{2}).$$ The first thing that had to be done was to find a way and understand how to solve the equations of motion for a massless particle (photon), since this would be the base for all the rest of our work. So, from the metric we can get the following equations (we could also use the Lagrangean to find the equations of motion), using \(\theta = \pi/2\) and having \(b\) as an impact parameter $$\left\{\frac{1}{r^{2}}\left(\frac{dr}{d\phi}\right)^{2}\right\} + \frac{1}{r^{2}}\left(1-\frac{2M}{r}\right) = \frac{1}{b^{2}},$$ and with \(u = 1/r\)
$$\left(\frac{du}{d\phi}\right)^{2} = 2Mu^{3} - u^{2} + \frac{1}{b^{2}}.$$Solving this equation we can find the lightlike geodesics we are interested in, as shown in the figure bellow.
Following our reference, we can also find some expressions useful for finding level curves (contours) of the accretion disk surrounding our Black Hole. To do this, we need to perform some quite lenghty calculations and to define new variables \(b = P^{3} / (P-2M)\), \(Q^{2} = (P-2M)(P+6M)\), that relates our impact parameter \(b\) to the periastron distance \(P\). With this, and solving some elliptical integrals, we can get
$$\cos \gamma = \frac{\cos \alpha}{(\cos(\alpha)^2 + \cos(\theta_0)^2)^{1/2}}$$
The observer will register BH's image over the photographic plane where the coordinates of each pixel is given in cylindrical coordinates \(b,\alpha\), where \(b\) is the impact parameter and \(alpha\) is the polar angle on the plane.
$$\frac{1}{r} = -\frac{Q - P + 2M}{4MP} + \frac{Q - P + 6M}{4MP} sn^{2}\left\{\frac{\gamma}{2}\sqrt{\frac{Q}{P}} + F(\xi_{\infty}, k)\right\},$$
and use this expression to find contours as the following.
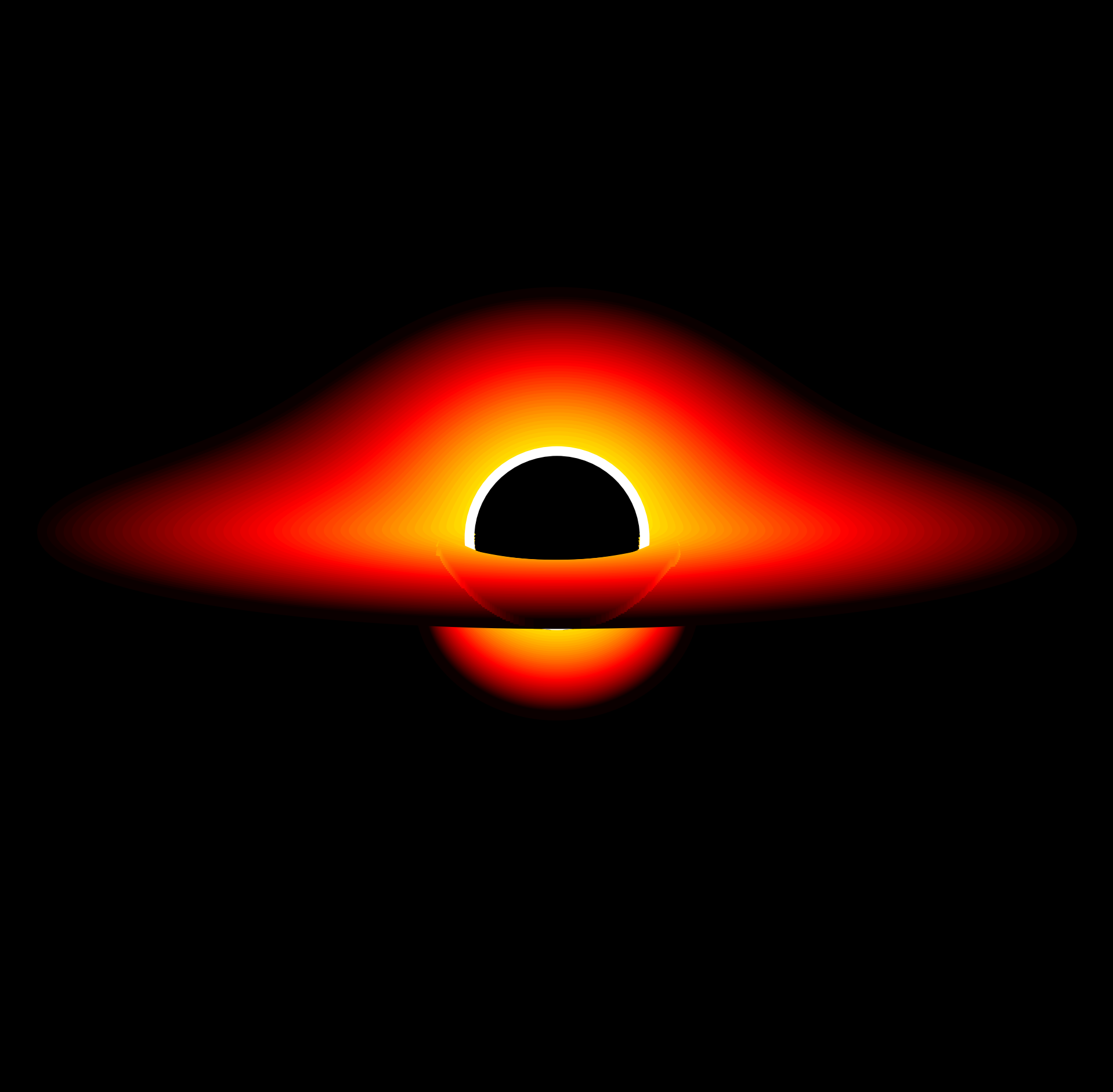
So everything that we did so far has already helped us to have a glance at how the physics works in our system, and how and observer would see it, in a way. Now, what if we would like to get a picture of the black hole, and not only the contours of our level curves? We need to find a way to popagate the photons of the accretion disk of the black hole up to the observer, and luckly, there are already some results that can help up. Page and Thorne [2] found the flux of radiation from the surface of the disk, given by
$$F_{s} = \frac{3M\dot{M}}{8\pi}\frac{1}{(r^* - 3)r^{*5/2}}\left[ \sqrt{r^{*}} - \sqrt{6} + \frac{\sqrt{3}}{3}log\left\{ \frac{(\sqrt{r^{*}} + \sqrt{3})(\sqrt{6} - \sqrt{3})}{(\sqrt{r^{*}} - \sqrt{3})(\sqrt{6} + \sqrt{3})} \right\} \right],$$ where \(\dot{M}\) is the accretion rate and \(r^{*}\) is the radius of the gas element. However that is not going to be the observed flux for our spacial photographer. To find the flux that he is going to measure we need to take into account the loss of energy suffered by each photon redshift, the lower measured rate of arrivel of photons due to time dilation and the relativistic correction to solid angle measurements. In the end, the real observed flux is going to be $$F_{s}^{real} = \frac{F_{s}}{(1+z)^{4}}.$$ For a photon emmited by a gas element the \(1+z\) can be calculated as $$1+z = (1-3\frac{M}{r})^{-1/2}(1+\left(\frac{M}{r^{3}}\right)^{1/2}b\sin(\theta)\sin(\alpha).$$ With this in mind, to create the photograph we need to choose a point in the accretion disk, calculate the flux, and map it in the photographic plate (what the observer sees) according to all of the dynamics described above,